Trajectory Optimisation in Learned Multimodal Dynamical Systems via Latent-ODE Collocation
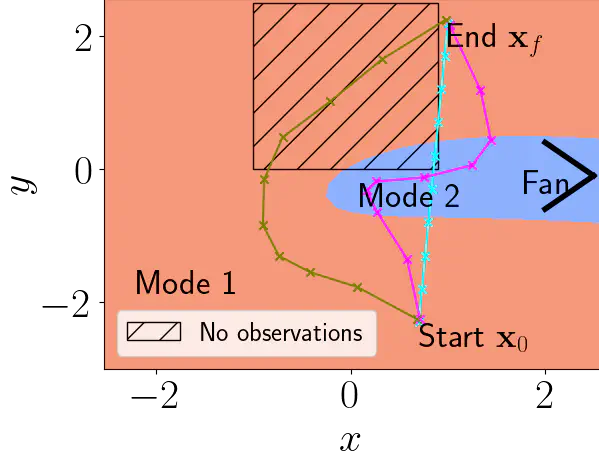 Image credit: Unsplash
Image credit: UnsplashAbstract
This paper presents a two-stage method to perform trajectory optimisation in multimodal dynamical systems with unknown nonlinear stochastic transition dynamics. The method finds trajectories that remain in a preferred dynamics mode where possible and in regions of the transition dynamics model that have been observed and can be predicted confidently. The first stage leverages a Mixture of Gaussian Process Experts method to learn a predictive dynamics model from historical data. Importantly, this model learns a gating function that indicates the probability of being in a particular dynamics mode at a given state location. This gating function acts as a coordinate map for a latent Riemannian manifold on which shortest trajectories are solutions to our trajectory optimisation problem. Based on this intuition, the second stage formulates a geometric cost function, which it then implicitly minimises by projecting the trajectory optimisation onto the second-order geodesic ODE; a classic result of Riemannian geometry. A set of collocation constraints are derived that ensure trajectories are solutions to this ODE, implicitly solving the trajectory optimisation problem.