Bayesian Learning for Control in Multimodal Dynamical Systems
Abstract
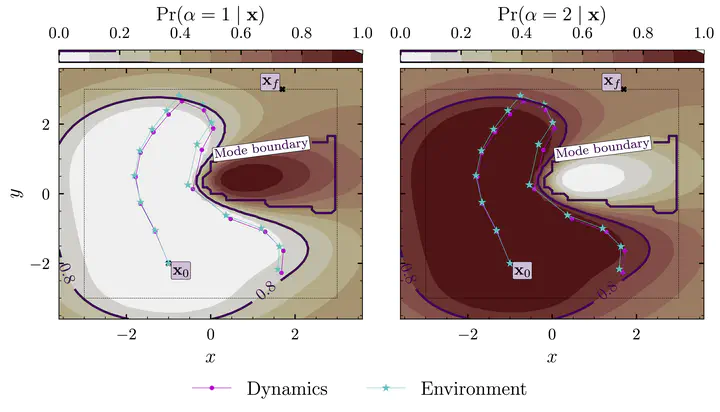
Over the last decade, learning-based control has become a popular paradigm for controlling dynamical systems. Although recent algorithms can find high-performance controllers, they typically only consider unimodal systems and cannot correctly identify multimodal dynamical systems. The main goal of this thesis is to control unknown, multimodal dynamical systems, to a target state, whilst avoiding inoperable or undesirable dynamics modes. Further to this, deploying learning algorithms in the real world requires handling the uncertainties inherent to the system, as well as the uncertainties arising from learning from observations. To this end, we consider the model-based reinforcement learning (MBRL) setting, where an explicit dynamics model – that includes uncertainties – is used to plan trajectories to a target state.
Motivated by synergising model learning and control, we introduce a Mixtures of Gaussian Process Experts (MoGPE) method for learning dynamics models, which infers latent structure regarding how systems switch between their underlying dynamics modes. We then present three trajectory optimisation algorithms which, given this learned dynamics model, find trajectories to a target state with mode remaining guarantees. Initially, the agent’s dynamics model will be highly uncertain — due to a lack of training observations — so these algorithms cannot guarantee mode remaining navigation with high confidence. When this is the case, the agent actively explores its environment, collects data and updates its dynamics model. We introduce an explorative trajectory optimisation algorithm that explicitly reasons about the uncertainties in the dynamics model. As a result, it can explore the environment whilst guaranteeing that the agent remains in the desired dynamics mode with high probability. Finally, we consolidate the work in this thesis into a MBRL algorithm, which solves the mode remaining navigation problem, whilst guaranteeing that the controlled system remains in the desired dynamics mode with a high probability.