Mode-constrained Model-based Reinforcement Learning via Gaussian Processes

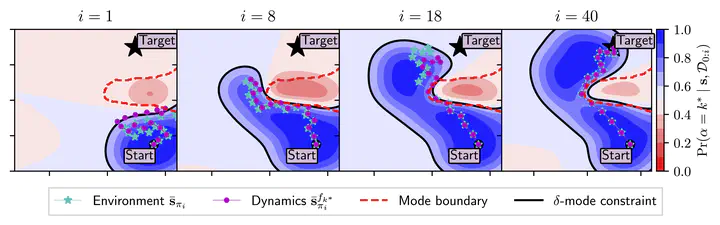
Abstract

Model-based reinforcement learning (RL) algorithms do not typically consider environments with multiple dynamic modes, where it is beneficial to avoid inoperable or undesirable modes. We present a model-based RL algorithm that constrains training to a single dynamic mode with high probability. This is a difficult problem because the mode constraint is a hidden variable associated with the environment’s dynamics. As such, it is 1) unknown a priori and 2) we do not observe its output from the environment, so cannot learn it with supervised learning. We present a nonparametric dynamic model which learns the mode constraint alongside the dynamic modes. Importantly, it learns latent structure that our planning scheme leverages to 1) enforce the mode constraint with high probability, and 2) escape local optima induced by the mode constraint. We validate our method by showing that it can solve a simulated quadcopter navigation task whilst providing a level of constraint satisfaction both during and after training.