Trajectory Optimisation in Learned Multimodal Dynamical Systems

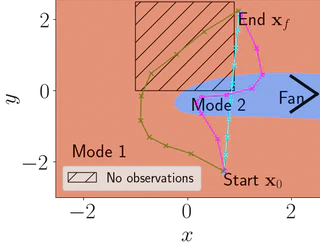
This work presents a two-stage method to perform trajectory optimisation in multimodal dynamical systems with unknown nonlinear stochastic transition dynamics. The method finds trajectories that remain in a preferred dynamics mode where possible and in regions of the transition dynamics model that have been observed and can be predicted confidently.

The first stage leverages a mixture of Gaussian process experts method (mogpe) written in GPflow/TensorFlow to learn a predictive dynamics model from historical data. Importantly, this model learns a gating function that indicates the probability of being in a particular dynamics mode at a given state location. In the second stage, this gating function acts as a coordinate map for a latent Riemannian manifold on which geodesics are solutions to our trajectory optimisation problem. Geodesics on this manifold satisfy a continuous-time second-order ODE. A set of collocation constraints are derived that ensure trajectories are solutions to this ODE, implicitly solving the trajectory optimisation problem. The trajectory optimisation is implemented in JAX.