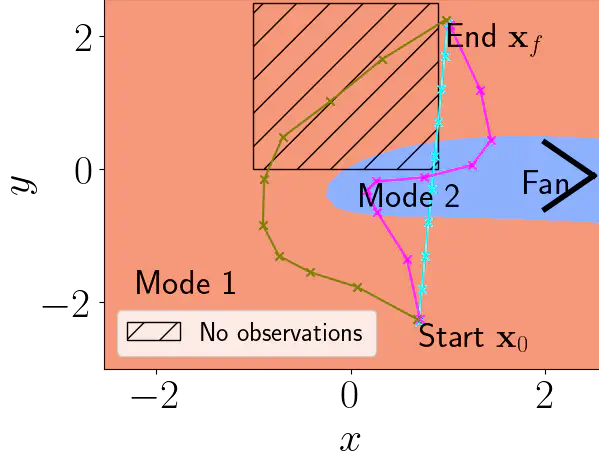
This work presents a two-stage method to perform trajectory optimisation in multimodal dynamical systems with unknown nonlinear stochastic transition dynamics. The method finds trajectories that remain in a preferred dynamics mode where possible and in regions of the transition dynamics model that have been observed and can be predicted confidently.
The first stage leverages a mixture of Gaussian process experts method
(mogpe) written
in GPflow/TensorFlow
to learn a predictive dynamics model from historical data.
Importantly, this model learns a gating function that indicates the probability of being in a particular
dynamics mode at a given state location.
In the second stage,
this gating function acts as a coordinate map for a latent Riemannian manifold on which
geodesics are solutions to our trajectory optimisation problem.
Geodesics on this manifold satisfy a continuous-time second-order ODE.
A set of collocation constraints are derived that ensure trajectories are solutions to this ODE,
implicitly solving the trajectory optimisation problem.
The trajectory optimisation is implemented in JAX.
Aidan Scannell
Postdoctoral Researcher
My research interests include model-based reinforcement learning, probabilistic machine learning (gaussian processes, Bayesian neural networks, approximate Bayesian inference, etc), learning-based control and optimal control.
