I am in the process of creating Jupyter notebooks for several probabilistic models and approximate inference algorithms. Particular focus has been put on providing detailed theory as well as easy to follow code.
So far I have created notebooks for Bayesian linear regression and Gaussian process regression. These can be found on my Github (probabilistic modelling).
Bayesian linear regression
I start by introducing regression and formulating linear regression as a Bayesian model, before deriving the parameters of the posterior distribution. The rest of the notebook then provides a well commented implementation of Bayesian linear regression.
Gaussian process regression
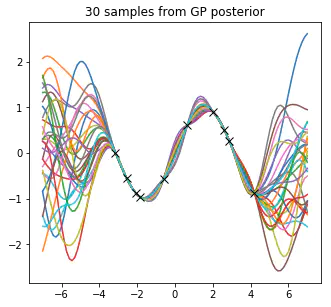
I start by defining the squared exponential (SE) kernel so that we can formulate our Gaussian process (GP) prior and then visualise it by drawing samples from it. We then define an underlying function that we are trying to recover, a sine function $\mathbf{y} = sin(\mathbf{x})$. From this we then generate a noise free input-output training data set and then formulate the joint distribution between the training targets and the test targets. We then condition our joint Gaussian prior distribution on the observations, which leads to the key predictive equations for Gaussian process regression. We then provide a practical algorithm for implementing Gaussian process regression and visualise our posterior. Next, we extend the model do deal with noisy observations, that is, $\mathbf{y} = sin(\mathbf{x}) + \epsilon$, where $\epsilon \sim \mathcal{N}(0, \sigma_n^2)$. Following this we apply Bayesian inference to Gaussian process regression in order to infer the hyper-parameters from the data, which provides automatic Ocam’s razor.